
Indicazioni su come vengono progettati i condotti dell’aria per impianti di ventilazione
Lo studio e il progetto dei canali d’aria per il condizionamento rappresentano una fase critica e imprescindibile nella progettazione di sistemi di ventilazione ed HVAC (Heating, Ventilation, and Air Conditioning) efficaci ed efficienti. L’importanza di una guida che fornisca istruzioni dettagliate su come condurre questo processo non può essere sottolineata abbastanza.
Innanzitutto, un’appropriata progettazione dei canali d’aria è essenziale per garantire che un edificio o un impianto sia adeguatamente rifornito di aria fresca e che l’aria condizionata venga distribuita in modo uniforme. Una guida che spieghi in dettaglio come condurre uno studio preliminare accurato e un progetto dei canali d’aria permette agli ingegneri e agli architetti di dimensionare correttamente i sistemi, evitando sovradimensionamenti o sottodimensionamenti che possono comportare sprechi energetici e costi aggiuntivi.
Progettazione adeguata
Inoltre, una progettazione adeguata dei canali d’aria è fondamentale per il comfort termico e la qualità dell’aria interna. Canali male progettati o mal posizionati possono causare dispersioni di temperatura e flussi d’aria irregolari, portando a condizioni di disagio per gli occupanti anche dovuti a rumorosità moleste. Una guida dettagliata può aiutare a minimizzare questi problemi, assicurando che l’aria venga distribuita in modo coerente e che i livelli di comfort termico siano ottimali.
Punto di vista energetico
Da un punto di vista energetico, l’efficienza di un sistema HVAC è direttamente correlata al progetto dei canali d’aria. Canali e condotti ben progettati riducono la perdita di carico e permettono una distribuzione dell’aria più efficiente, riducendo così il consumo di energia e i costi operativi a lungo termine. Questo è particolarmente importante nell’attuale contesto di crescente attenzione verso la sostenibilità ambientale e l’efficienza energetica.
Infine, una corretta progettazione dei canali d’aria contribuisce a garantire una qualità dell’aria interna ottimale. Questo è fondamentale per la salute e il benessere degli occupanti, in quanto una cattiva circolazione dell’aria può portare all’accumulo di agenti inquinanti e allergeni, con possibili conseguenze per la salute respiratoria.
In conclusione, una guida dettagliata su come effettuare lo studio e il progetto dei canali d’aria per il condizionamento è fondamentale per la corretta progettazione e l’efficace funzionamento dei sistemi HVAC. Questa guida realizzata da Itieffe, offre una base solida per garantire efficienza energetica, comfort, qualità dell’aria interna e risparmio a lungo termine, contribuendo così a creare ambienti più salubri, sostenibili e confortevoli.
Studio progetto canali aria
STUDIO E PROGETTO DEI CANALI D’ARIA
Per il calcolo di un impianto di ventilazione che necessita di condotti d’aria e necessario seguire un procedimento ordinato che può essere cosi schematizzato.
1) Uno studio attento della pianta dell’edificio e dell’edificio stesso. al fine di progettare l’impianto più conveniente. evitando per quanto possibile tutti gli ostacoli ed assicurando ogni necessario accesso alle sue parti componenti. Allo stesso tempo facendo in modo che il progetto sia semplice e che preveda curve ampie e variazioni graduali di sezione.
2) Una collocazione delle uscite dal condotto tale da garantire un’appropriata distribuzione dell’aria nell’ambiente da ventilare.
3) Determinare le dimensioni delle bocche d’uscita in base al volume d’aria necessario. al loro numero ed alla velocità consentita. al fine di ottenere ii lancio desiderato. non dimenticando. però, che all’aumentare della velocità aumenta anche il rumore ed assicurandosi che tutte le bocchette abbiano un’adeguata superficie libera.
4) Calcolare le dimensioni di tutti i condotti principali e delle diramazioni con uno dei due metodi seguenti:
- a) metodo basato sulla velocità: prestabilendo la velocità dell’aria nei diversi punti del circuito a partire dal suo massimo valore nel condotto principale al suo minimo allo sbocco nell’ambiente
- b) metodo basato sulla uguale resistenza: il condotto è proporzionato in modo da ottenere un’uguale perdita di pressione per attrito per unità di sviluppo del condotto.
VELOCITÀ DEL’ARIA NEI CONDOTTI
|
Posizione |
edifici civili m/s |
ambienti industriali m/s |
|
Prese aria fresca |
4 – 5 |
6 – 8 |
|
Condotto principale collegato al ventilatore |
4 – 5 |
6 – 12 |
|
Diramazioni del condotto |
2 – 5 |
3 – 6 |
|
Diramazioni verticali |
1,5 – 3 |
2 – 4 |
|
Bocchette, griglie, ecc. |
0,5 – 2 |
1 – 5 |
Negli ambienti industriali sono ammesse velocità maggiori dell’aria, perché il rumore che ne deriva è un fattore trascurabile.
Analoga considerazione può essere fatta per altri particolari ambienti. Normalmente, la distribuzione dell’aria dal ventilatore alle bocche d’uscita viene effettuata, prima con un collettore principale e poi con singole diramazioni, piuttosto che con più canalizzazioni facenti capo separatamente al ventilatore, e ciò per ovvie ragioni di economia sul costo dell’impianto.
METODO BASATO SULLA VELOCITÀ
Tale metodo, per stabilire le dimensioni dei condotti d’aria, implica la scelta arbitraria delle velocità nelle differenti sezioni dell’impianto stesso partendo, come s’è detto, dalle velocità più alte vicino al ventilatore per arrivare, con riduzioni progressive, alle velocità più basse nelle varie diramazioni e quindi nelle griglie o bocchette che immettono l’aria nell’ambiente da ventilare.
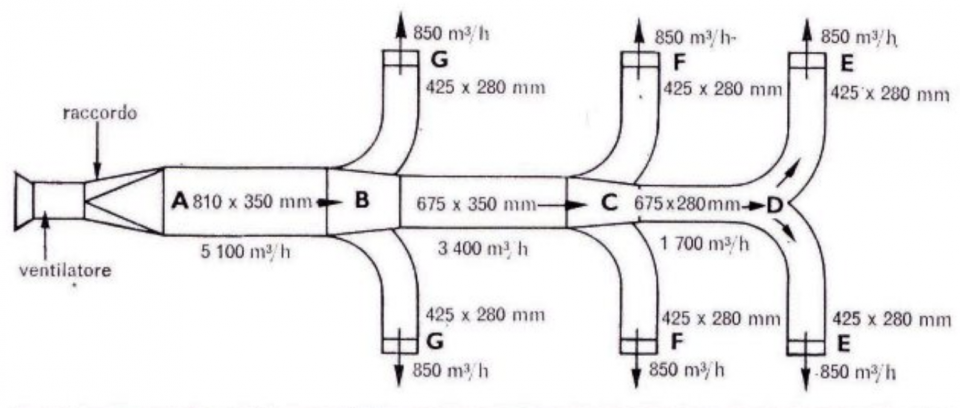
Esempio 1
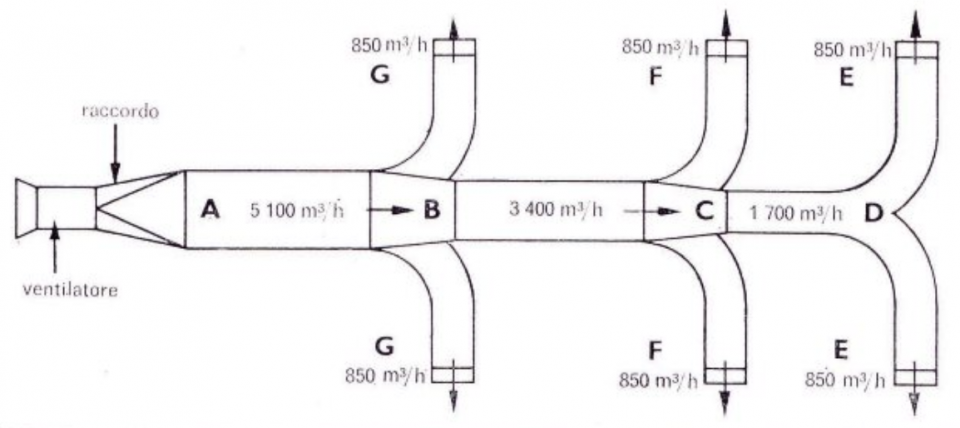
Nella figura 1 è illustrato un impianto semplice, previsto per un ambiente civile, provvisto di sei bocchette d’immissione da 850 m3/h ciascuna nei punti EE, FF, GG.
L’impianto, perciò, sarà calcolato per una portata totale d’aria di 6 x 850 = 5.100 m3/h.
Il condotto principale sia dato dai tratti A B C D.
Sezione AB del condotto principale
Questa sezione porta 5.100 m3/h ed ammettendo che il rumore sia un fattore trascurabile, la velocità in questo tronco può essere di 5 m /s.
Superficie della sezione AB

Sezione BC del condotto principale
Qui il fattore rumore diventa più importante ed e bene adottare una velocità di 4 m/ s. Questa sezione porta 5.100 m3/h, meno l’aria derivata nei due bracci BG, cioè 5.100 – 1.700 = 3.400 m3/h.
Superficie della sezione BG
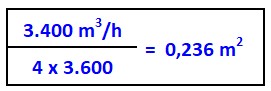
Sezione CD del condotto principale
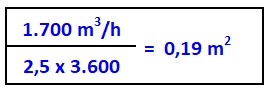
Poiché questa sezione del condotto principale è lontana dal ventilatore ed alimenta soltanto i due bracci DE. la velocità appropriata e 2,5 m /s.
Questa sezione porta 5.100 m3/h meno l’aria derivata nei quattro bracci BG e CF, cioè 5.100 – (1700 – 1.700) = 1.700 m3/h.
Superficie della sezione CD
Derivazione DE
Poiché ad ogni derivazione c’è solo un’uscita E, i due tronchi di condotto avranno le stesse dimensioni ed ammettendo che la velocità più appropriata sia 2 m/s per una portata di 850 m3/h avremo:
Superficie della sezione DE

Ora, note le aree delle sezioni dei condotti, se ne possono stabilire le dimensioni effettive tenendo presente che per facilità di costruzione è opportuno, in corrispondenza di ogni variazione di sezione, variare una sola delle due dimensioni.
Nell’esempio considerato le dimensioni adatte potrebbero essere:
AB = 810 X 350 mm = 0,283 m2
BC = 675 X 350 mm = 0,236 m2
CD = 675 X 280 mm = 0,189 m2
DE = 425 X 280 mm = 0,119 m2
METODO BASATO SULLA UGUALE RESISTENZA
Tale metodo, per stabilire le dimensioni dei condotti d’aria, è probabilmente migliore del metodo precedente; esso si prefigge di garantire una buona distribuzione soprattutto in quegli impianti che hanno un notevole sviluppo in lunghezza.
Con esso, inoltre, non è necessaria, almeno fino ad un certo punto, una certa esperienza per determinare le velocità più idonee nelle diverse parti dell’impianto; soltanto una velocità deve essere stabilita a priori: quella nell’ultimo tronco del sistema.
Fissate le dimensioni di questo tratto, le altre velocità vengono calcolate in modo tale da avere la stessa caduta di pressione per unità di lunghezza del condotto.
Il diagramma della figura 4. dà la perdita di pressione in mm c.d.a. [o kg/m2) per condotti circolari di differenti dimensioni e che trasportano le quantità d’aria indicate; vi si può leggere la caduta di pressione per una data sezione e, quindi, si possono stabilire le dimensioni degli altri tratti di condotto leggendo il diametro corrispondente alla stessa caduta di pressione in base alla rispettiva portata d’aria.
In base alla tabella 1. si possono altresì ricavare i diametri dei condotti circolari equivalenti, note le dimensioni dei lati dei condotti rettangolari e viceversa.
Esempio 2
A partite dal condotto DE, considerato nell’esempio già citato, e supponendo una velocità di 2 m/s:
dimensioni del condotto:

Diametro del condotto circolare equivalente = 0,388 m.
Dal diagramma della figura 4, la caduta di pressione per 1 m di condotto risulta uguale a 0,013 mm c.d.a.
Il condotto CD porta 1700 m3/h, la caduta di pressione per una lunghezza di 1 m sia 0,013 mm c.d.a.
Diametro del condotto equivalente circolare = 500 mm.
Il condotto BC porta 3.400 m3/h, la caduta di pressione per 1 m sia sempre 0,013 mm c.d.a.
Diametro del condotto circolare equivalente = 650 mm.
Il condotto AB porta 5.100 m3/h, la caduta di pressione per I in sia sempre 0,013 mm c.d.a.
Diametro del condotto circolare equivalente = 770 mm.
Abbiamo così stabilito le dimensioni dei canali, supponendo che essi siano costituiti da condotti a sezione circolare. Per ottenere i corrispondenti condotti rettangolari ci si potrà servire della tabella l adottando le seguenti proporzioni.
|
Condotto |
Ø mm |
Condotto rettangolare equivalente approssimato |
|
DE Ø |
388 |
400 X 320 |
|
CD Ø |
500 |
680 X 320 |
|
BC Ø |
650 |
680 X 520 |
|
AB Ø |
770 |
960 X 520 |
E bene tener presente che questo metodo stabilisce semplicemente le dimensioni dei condotti dell’impianto; da ciò non consegue automaticamente che ad ogni bocchetta si abbia l’esatta quantità d’aria prefissata.
Le uscite più vicine al ventilatore potranno dare un po’ più d’aria che quelle situate alle estremità dell’impianto.
In tal senso un progetto più preciso dell’impianto comporterebbe lunghi calcoli e, con tutta probabilità, dimensioni frazionate dei condotti.
Nei casi in cui è essenziale un‘esatta distribuzione dell’aria, è del tutto normale ricorrere a serrande che consentano di regolare le portate nelle singole derivazioni.
Infine, bisogna porre molta attenzione nel dimensionare curve, cambiamenti di sezione, nel valutare gli ostacoli, ecc., al fine di mantenere la caduta di pressione nell’impianto la più bassa possibile e conseguire risparmio di potenza nell’azionamento del ventilatore.
Nella figura 3. sono dati alcuni esempi d’elementi costituenti gli impianti di ventilazione nelle loro possibili situazioni.
CONVERSIONE DI PRESSIONE DINAMICA IN PRESSIONE STATICA
In molti casi, il ventilatore scelto per una data rete di canalizzazioni è un piccolo ventilatore ad alta velocita di rotazione e ad elevate velocita di mandata dell’aria.
Ciò comporta una pressione dinamica e quindi un’energia cinetica elevate.
In questi casi è: opportuno che questa energia sia riutilizzata per aumentare la prestazione del ventilatore piuttosto che lasciarla disperdere.
Ciò si può conseguire se, prima dello scarico finale dell’aria, si farà in modo di ridurre convenientemente la velocità dell’aria stessa con un minimo di perdita, fino ad ottenere che la pressione dinamica sia ragionevolmente bassa.
L’energia cosi recuperata data incremento alla pressione statica sviluppata dal ventilatore.
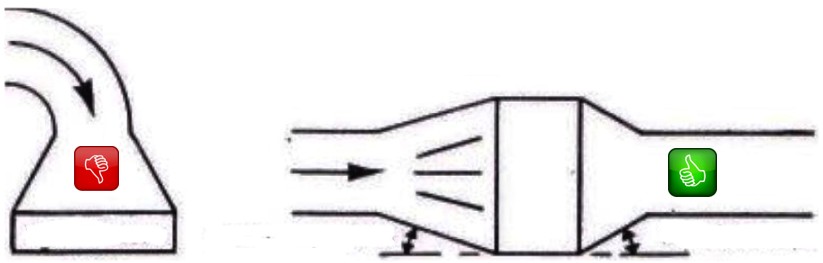
Praticamente ciò si ottiene con l’impiego di un condotto divergente, detto diffusore, avente un diametro finale funzione della velocità di scarico desiderata.
L’angolo di divergenza e importante; da esso dipendono le possibilità di recupero dell’energia cinetica, ma non sono da trascurare lo spazio occupato ed il costo del diffusore stesso.
In generale si può dire che in un diffusore l’angolo totale di divergenza non dovrebbe superare i 10° per ottenere un buon recupero, mentre risulta del tutto inutile se la sua apertura è di 60° o più.
Il diagramma della figura 5 indica le proporzioni e le dimensioni ottimali, per diffusori posti sulla mandata di un ventilatore, corrispondenti a differenti percentuali di recupero della pressione dinamica del ventilatore.
Lo stesso principio si può applicare quando il ventilatore non scarica a bocca libera, ma alimenta una rete di condotti, con la differenza che la pressione dinamica dell’aria in movimento non si perde all’estremità del diffusore ma si mantiene nel condotto che lo segue.
Di conseguenza qualsiasi recupero di pressione statica è dovuto alla differenza di pressione dinamica alle due estremità del diffusore stesso.
La figura 6. indica la percentuale del recupero di pressione statica nel diffusore in base alla differenza di pressione dinamica a ciascuna delle sue estremità, quando non vi sono perdite allo scarico.
Esempio 3
Un impianto con aria canalizzata è: previsto per il convogliamento di 8.500 m3/h alla pressione statica di 18 mm c.d.a. Si vuole utilizzare un ventilatore assiale con ventola a pale con profilo alare da 480 mm di diametro circa con:
una portata di 8.500 m3/h, una pressione statica di 13 mm c.d.a. ed una pressione totale di 23 mm c.d.a. Quali sono le dimensioni del diffusore necessarie per ottenere la pressione statica voluta di 18 mm c.d.a.?
Pressione dinamica = Pressione totale — Pressione statica: 23 — 13 = 10 mm c.d.a.
Recupero di pressione statica voluto = 18 — 13 = 5 mm.
Se il ventilatore si trova completamente a valle dell’impianto, cioè scarica a bocca libera, la percentuale di recupero richiesta sarà:

Dalla figura 5 le dimensioni ottimali di un diffusore che dia un recupero del 50 % risultano essere:
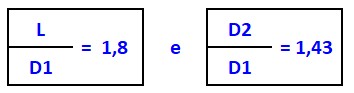
dove:
L = lunghezza del diffusore
D1 = diametro dell’estremità del diffusore (lato ventilatore)
D2 = diametro dell’estremità del diffusore (lato scarico)
e quindi:
L = 1,80 X 480 mm = 865 mm circa
D = 1,43 X 480 mm = 685 mm circa.
Figura 3
ESEMPI DI DISTRIBUZIONE CORRETTA ED ERRATA DI PARTI DI CONDOTTI ARIA
Entrata nel condotto

Riduzione ed allargamento di sezione

Curve e derivazioni
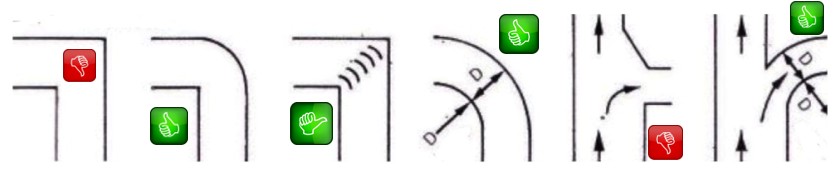
Tabella 1
Canali aria – diametro equivalente

Figura 4
Perdite di carico in tubazioni diritte circolari in lamiera zincata – aria a 20°C e 760 mm Hg
Portata in m3/h
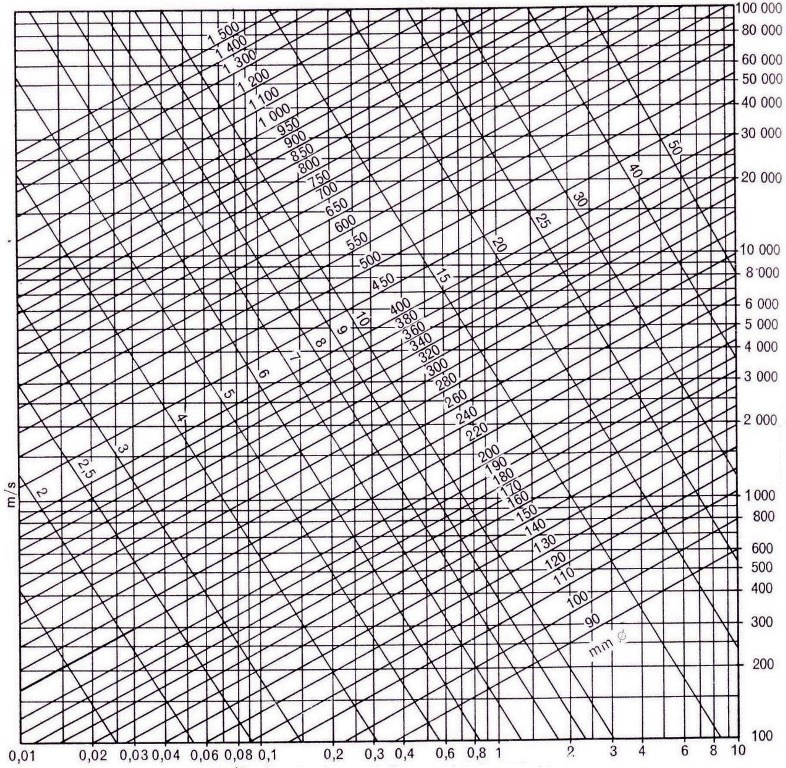
Figura 5
Dimensioni ottimali diffusori in mandata di un ventilatore per differenti percentuali di recupero di pressione dinamica
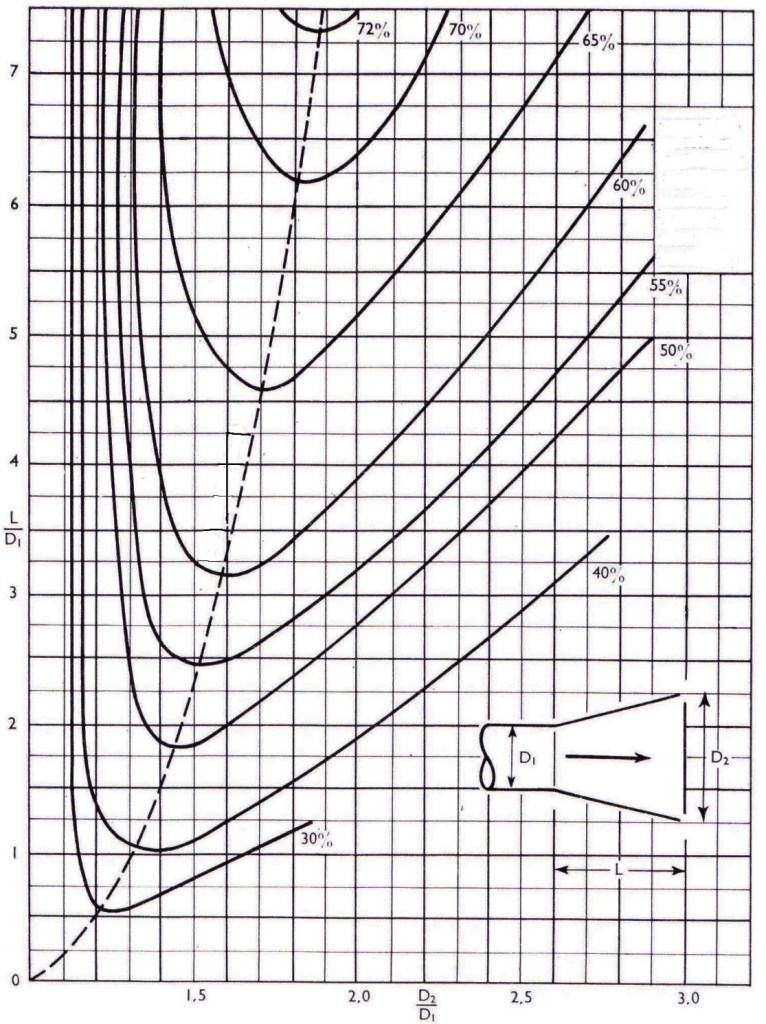
Recupero di pressione statica in % della pressione dinamica nella sezione D
Figura 6
Recupero in pressione statica espresso in % sulla differenza tra le pressioni dinamiche alle due estremità del diffusore
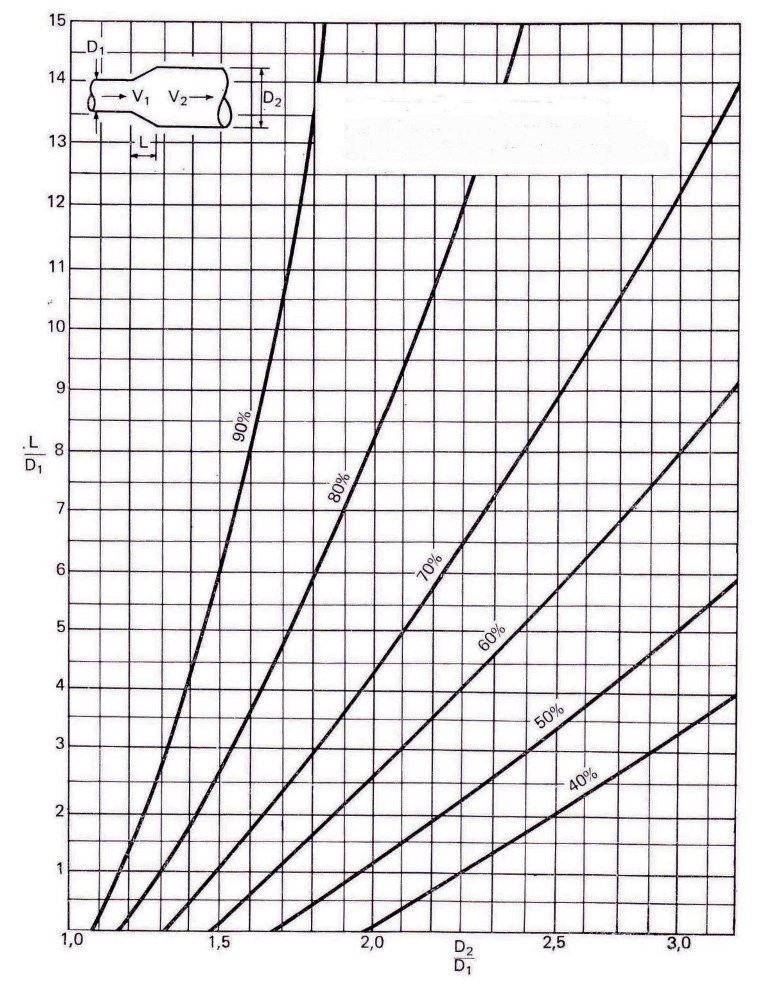
Recupero di pressione statica nei diffusori espresso in % sulla differenza delle pressioni dinamiche
Altri programmi gratuiti dello stesso genere offerti da itieffe ▼
- Condizionamento aria
- Canalizzazioni aria
- Sistemi di ventilazione
- Condizionatori autonomi
- Diagrammi psicrometrici
- Tabelle condizionamento aria
- Qualità dell’aria
- Schemi & disegni condizionamento
